Hey Berend en Joris,

Helaas heb ik nooit met IP Coach gewerkt, hier weet ik dan ook niet zo veel van. Daarom kan ik jullie alleen helpen de sprong wiskundig te beschrijven. Ik zal dit puntsgewijs doen (van hoog naar laag):

Op 39 km hoogte Baumgartner springt naar beneden en valt achtereenvolgens door:

39 km - 32 km : Eerste laag stratosfeer
32 km - 20 km : Tweede laag stratosfeer
20 km - 11 km : Derde laag stratosfeer (temperatuur blijft gelijk)
11 km - 0 km: Troposfeer

In elk van de bovenstaande lagen (behalve in de derde laag van de stratosfeer) varieert de temperatuur en de dichtheid met de hoogte. De dichtheid is belangrijk, omdat de luchtweerstand hier vanaf hangt.

De eerste aanname die ik zou maken is dat er slechts twee krachten op Baumgartner werken: de zwaartekracht en de weerstandskracht. Beiden staan lijnrecht tegenover elkaar. Zonder deze aanname wordt het al gauw veel te ingewikkeld.

De formule voor zwaartekracht weet je als het goed is en de formule voor de weerstandskracht is:

In deze formule zul je Cd en A moeten schatten. Dit zijn respectievelijk de weerstandscoëfficiënt en het oppervlak (loodrecht op de weerstandskracht) van een mens. Rho en v (dichtheid en snelheid) ondergaan verandering gedurende de val. De formule voor v is als volgt:

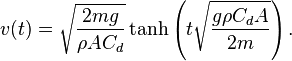
Deze formule vind je hier. Waar g de valversnelling is (9.81 m/s2) en t de tijd in seconden. Massa m zul je ook moeten schatten (of je moet de massa van Baumgartner ergens op internet kunnen vinden). Overigens is tanh (dus niet tan h!) een hyperbolische functie van de tangens (heb je waarschijnlijk nog niet geleerd). Meer informatie vind je hier. In de formule vind je opnieuw Rho terug. De formule voor Rho (afhankelijk van hoogte) is de volgende:

Rho = Rho(0) * e^((-gh)/(RT))

In deze formule is Rho(0) de dichtheid op zeeniveau, R de gasconstante en T de temperatuur (in Kelvin). Deze formule heb ik kunnen vinden in een van mijn studieboeken (Introduction to Flight van John D. Anderson - pagina 125), maar ik denk dat als je goed zoekt op internet dat je hem daar ook wel zult vinden.

T in de formule is ook afhankelijk van de hoogte. Voor elk van de 4 lagen die ik hierboven al genoemd heb geldt een andere formule:

Eerste laag stratosfeer: T = T(39km) - 0.0028 * delta h
Tweede laag stratosfeer: T = T(32km) - 0.001 * delta h
Derde laag stratosfeer (temperatuur en dichtheid blijven gelijk): T = constant = T(20km) = T(11km)
Troposfeer: T = T(11km) + 0.0065 * delta h

De eenheid van temperatuur is in alle gevallen Kelvin [K]!

Meer over deze waarden en de veranderende temperatuur in de atmosfeer vind je hier.

Als laatste is er natuurlijk ook een verband tussen de hoogte en de snelheid. Die formule kun je zelf afleiden:

delta h = 0.5 * (Veind + Vbegin) * delta t

Des te kleiner je de delta t neemt des te nauwkeuriger zal je model worden. Als je alle formules bij elkaar brengt zie je dat er een soort algoritme ontstaat. Belangrijk is dat je eerst een delta t (bijvoorbeeld 0.5 seconden) bepaalt en vervolgens met alle geschatte waarden en de dichtheid op 39 km hoogte een snelheid berekent (Veind). Vervolgens kun je een delta h berekenen en ga je alle formules naar boven weer af totdat je weer bij de formule voor de snelheid bent. Dan begin je weer opnieuw (of in dit geval IP Coach). Let op dat zodra er een bepaalde snelheid wordt bereikt zodat Fz = Fd. Vanaf dat moment blijft de snelheid namelijk gelijk.

Al met al is de simulatie van zo'n val best een lastig proces en vergt het veel denkwerk. Zeker als je ook nog rekening gaat houden met z'n parachute. Ik hoop in ieder geval dat jullie hier wat mee kunnen. Mocht je nog vragen hebben, stel ze hier, dan zal ik ze dit keer wel snel behandelen ;)

Groetjes,
Wouter

Hallo Michiel,

Wij hebben gisteren onze proef uitgevoerd en hebben ook nog de onderzoeksreactor bezocht. We hebben een waanzinnig leuke dag gehad en we zijn weer een heel eind op weg met ons profielwerkstuk. Bij deze nogmaals bedankt voor al je hulp!

Met vriendelijke groet,

Rianne

Hoi Dennis,

Goed nieuws. Wij hebben hier op de TU een hele goede opstelling voor holografie waar ook al eerder middelbare scholieren mee hebben gewerkt. Bovendien heb ik iemand gevonden die er veel verstand van heeft en je zou kunnen begeleiden. Het gaat om een complete optische opstelling voor transmissie holografie met een rode laser van 633 nm. Zou jij komende tijd, tijd hebben om langs te komen? Voor kerst of tussen kerst en oud&nieuw? Dan kun je naar de opstelling kijken en een dag plannen met de begeleider wanneer je dan echt een hologram kan gaan maken.

Ik zal je ook wel even per email benaderen.

Groet,
Michiel

Hoi Gertjan en Math,

Ik neem aan dat jullie met gassamenstelling, de samenstelling van de uitlaatgassen bedoelen. Ik weet niet zeker of we dat kunnen meten, maar we zullen sowieso niet jullie brommers direct aan meetapparatuur aan kunnen sluiten (aangezien dit niet een standaard opstelling bij ons is). Kunnen jullie nadenken over een manier om de gassen te 'vervoeren'. Je zou bijvoorbeeld de gassen door een vloeistof kunnen leiden, een deel zal oplossen in het oplosmiddel en vervolgens kunnen we hier concentraties van meten. Wat zou een geschikt oplosmiddel kunnen zijn? Of misschien hebben jullie een ander idee?

Ik hoop jullie een stapje verder te hebben geholpen!

Hallo Marc en Luc,

Excuses voor de late reactie. Omdat dit onderwerp is geplaatst in het Natuurkunde proefjes forum in plaats van bij de raketten is het tussen mijn vingers door geglipt.

Zoals ik in de mail al heb aangegeven hebben we een windtunnel tot onze beschikking die we een aantal keren per jaar een dag mogen gebruiken. Tijdens die dagen voeren we workshops uit zodat we zo veel mogelijk scholieren tegelijkertijd helpen. De meeste vraag is naar de liftkracht en vorm van vleugels, vandaar dat ook de workshop daar over gaat.

Zoals ik al had verteld bestaat de opstelling uit een frame waarbij je lift kunt meten. Heel af en toe wordt de opstelling aangepast om ook weerstand te meten, maar dat is volledig afhankelijk van het onderzoek wat er op dat moment wordt uitgevoerd in de tunnel. Afhankelijk hoe de opstelling er uit ziet en of onze modellen er op passen worden deze vervolgens voor ons aangepast zodat wij op de workshop van de tunnel gebruik van kunnen maken. Helaas ligt het niet in mijn handen om hier invloed op te hebben.

Als jullie interesse hebben om een workshop te volgen in januari of februari, wil ik jullie graag vragen om het interesse formulier op de windtunnel pagina in te vullen. De workshop van aanstaande week (5 december) is in principe als gesloten voor inschrijving, maar er is om 9 uur 's ochtends nog een plek vrij. Mochten jullie daar deel aan nemen, is het het handigst als jullie me dit via de mail laten weten, dan kan ik jullie nog indelen.

Groet,

Hubert

Hallo Leon en Yoël,

We hebben eens in de twee maanden een windtunnel tot onze beschikking waar we workshops geven. Helaas is deze windtunnel niet groot genoeg voor jullie experiment. De test sectie is rond en heeft een diameter van ongeveer 60 cm. De volgende workshop op 5 december is helaas al vol, maar mochten jullie alsnog interesse hebben om een workshop te volgen dan zou je het interesse formulier kunnen invullen (op de windtunnel pagina). De workshop zelf gaat over vleugelprofielen, dat zit dus in het verlengde van jullie onderwerp maar het gaat dus niet specifiek om windmolens.

Groet,

Hubert

Ha jongens,

Ik heb net de goede contactgegevens van de persoon die over het nevelvat van de studievereniging gaat dus ik ga toch nog even vragen hoe en wat. Ik hou jullie op de hoogte mochten jullie toch, bij goed nieuws, weer terug willen ruilen. Hou deze topic dus nog even in de gaten. Ondertussen moeten jullie je zeker inschrijven voor de windtunnel workshop op 5 december. Ik zou jullie graag bij dit onderwerp begeleiden, maar er is een medestudent Hubert, die de workshop geeft en lucht en ruimtevaart studeert, die jullie daar veel beter mee kan begeleiden. Voor vragen kunnen jullie terecht bij het forum onder het kopje "Raketten, vliegtuigen & aerodynamica".

Succes jongens!
Groet,

Michiel

Inschrijven: http://scholierenlab.tudelft.nl/practicum/workshop/windtunnel/

Hoi Tim,

Om proeven te doen met supergeleiding en het meissner effect is vloeibare stikstof nodig en dat is gevaarlijk spul em moeilijk om aan te komen. Daarom raad ik je aan woensdag 12 december s middags naar de TU Delft te komen. Ik hou dan een workshop over supergeleiding waar ik het een en ander uitleg en begeleid bij experimenten. Klik hier voor meer info en inschrijven.

Groetjes,

Michiel

Hoi Tycho,

Antigeluid vraagt erom dat je exact hetzelfde geluid in het faseverschil van exact een halve periode afspeelt, zodat het elkaar uitdempt. Als je geluid met een microfoon opneemt en direct weer afspeelt met je laptop gebeuren er ondertussen een hoop dingen die voor vertraging van het signaal zorgen (bijvoorbeeld signaal conditionering en analoog-digitaal en digitaal-analoog conversies). Je kan dit inderdaad proberen door te spelen met de vertraging, maar je hebt kans dat je signaal sowieso een beetje vervormd eruit komt.

Dus ik hoop dat het lukt met een beetje delay, je kan deze software ervoor gebruiken: http://www.daansystems.com/radiodelay/.

Nog een tip: hoe hoger je frequentie, hoe moeilijker het is om exact de juiste fase te vinden, dus probeer het anders ook een keer met 20-30 Hz.

Succes en ik hoor graag of het lukt!

Hoi Maarten,

Afgelopen twee workshops mochten we een opstelling van een afstudeerder gebruiken die het mogelijk maakte om ook de weerstand te meten. Helaas is het zo dat ik dat dus niet kan garanderen voor de workshop van 5 December. Ik kan je helaas pas een week van te voren laten weten of die opstelling weer wordt gebruikt. Onze eigen opstelling is gebouwd om de draagkracht te meten, daar heb jij bij een raket helaas weinig aan.

Wat je dus wel kunt doen is naar de stabiliteit van je raket kijken. Dit zou je kunnen doen door een staaf door je raket te plaatsen die als een soort draaipunt gaat werken...

Hoi,

Je hoort het niet vaak, een PWS over kwantum, maar een erg leuk onderwerp. Naar mijn mening het meest veelbelovende stukje natuurkunde. De TU Delft is heel actief met ontwikkelen van voorlopers van quantum computers, maar helaas heeft het science centre niet veel te bieden op dit gebied. Ook de experimenten bij ons op natuurkunde die verband hebben met kwantummechanica zijn waarschijnlijk niet voor jullie toegankelijk, omdat het zeer kostbare en kwetsbare opstellingen zijn. Bovendien zijn ze veelal continu in gebruik.

Kwantummechanica gaat van een theorie uit dat deeltjes, zoals fotonen (lichtquanta of lichtdeeltjes) en elektronen, af en toe eigenschappen van een deeltje en af en toe eigenschappen van een golf vertonen. Bij het doublesplit experiment bewijst men door interferentie (een verschijnsel dat alleen bij golfen plaatsvindt) te laten zien bij fotonen (door een laser te gebruiken) of elektronen (door een e-gun te gebruiken) dat het om golven gaat. Als je dan ook nog bewijs heb dat het deeltjes betreft heb je dus in feiten bewezen dat het om golf en deeltjes tegelijkertijd gaat. Zie de wikipedia over het tweespletenexperiment, een youtube filmpje van Dr Quantum, die heel veel goede quantum filmpjes op youtube hebt en een handleiding (en nog een om het experiment zelf uit te voeren.

Als jullie wat verder in het proces zijn en hoofd en deelvragen of een opzet voor een eigen experiment hebben, help ik jullie graag wat verder en zouden jullie eventueel op het forum of langs kunnen komen zodat jullie mij wat extra vragen kunnen stellen als jullie die hebben!

Succes!

Yanick,

Zou je mij een PM kunnen sturen? Dan heb ik je emailadres en kan ik je contactgegevens doorsturen aan een docent op onze faculteit. Hij wil graag weten wat je precies voor plannen hebt.

Gr,
Noor

Hey Jurriaan,

21 november 2013 was een foutje, het is 2012. Over precies een maand zal de workshop dus plaatsvinden!

Groeten Thijs

Hoi Dick,

Het steriliseren van voedsel met straling wordt doorstralen genoemd. Beknopte informatie daarover is te vinden op wikipedia (de Engelse wikipedia is veel uitgebreider met bronnen en risico's dus probeer die ook door te nemen). Bestralen gebeurt op twee verschillende manieren: gammastraling en rontgenstraling (even klikken voor info over bijvoorbeeld waar de straling vandaan komt). Beiden vormen van ioniserende straling en beiden methoden hebben hetzelfde effect: DNA van micro-organismen in het te bestralen voedsel wordt kapot gemaakt, wardoor deze niet langer meer kunnen delen en dus vermeerderen.

Bestralen klinkt misschien gevaarlijk, maar het is simpelweg een vorm van een reactie teweeg brengen in het te bestralen voedsel. Net als wanneer je iets pasteuriseerd om te steriliseren of vervuild water kookt om microorganismen te doden voor je het drinkt. Als je thuis je magnetron gebruikt bestraal je je voedsel eigenlijk ook, alleen dan met microgolfen die moleculen alleen laten trillen en niet kapot kunnen maken. De golflengte van gamma en alfa straling is namelijk anders en dus de energie ook, zie elektromagnetische straling en een eerder post op het forum.

Het grote gevaar bij stralen is echter dat de straling zelf ook DNA kapot kan maken in het menselijk lichaam, maar aangezien de straling slechts door het voedsel heen gaat is de straling er allang uit voordat het voedsel op je bord ligt. Belangrijk is dus wanneer het voedsel wordt bestraalt dat dit goed wordt afgeschermd zoals je ook in het ziekenhuis ziet bij een rontgenfoto.

Voor een proefje zou je eigenlijk moeten proberen om twee dezelfde stukken vlees of groente te krijgen en dan kijk of nadat je een wel bestraalt en de ander niet de een langer houdbaar blijft. Dit zou je met verschillende straling kunnen doen verschillende hoeveelheid straling en verschillende soorten voedsel. Probleem is alleen: hoe kom je aan de straling. Op de TU Delft gebruiken wij ioniserende straling, maar dit is erg gevaarlijk en alleen op onze kernreactor te vinden, dus ik ben bang dat je hier niet zo makkelijk bij kunt. Wel zou je bijvoorbeeld op bezoek kunnen gaan bij een bedrijf wat voedsel bestraald (even googlen) of even kunnen kijken of je misschien in een biosupermarkt kan kijken of je onbestraald voedsel kan vinden en dit kan vergelijken in houdbaarheid met bestraald voedsel.

Succes met je PWS
Groetjes,

Michiel

Beste Jeroen en Maarten,

Ik ga overleggen of hier ruimte voor is op de TU Delft. Maar hebben jullie zelf al nagedacht over wat jullie precies willen toevoegen? Als jullie een proef kunnen doen, is het belangrijk dat jullie wel zelf een heel plan hebben. Ik ben benieuwd waar jullie aan denken, dan kan ik jullie verder op weg helpen.

Ha Timke!

Leuk onderwerp! Zoals je misschien al weet bestaat licht uit fotonen. Dit zijn gewichtsloze deeltje die in een golf bewegen en altijd met dezelfde snelheid bewegen: de lichtsnelheid, de grootste snelheid mogelijk. Misschien heb je wel gehoord dat in september vorig jaar er bij het europese onderzoeksinstituut CERN een neutrino (fysisch deeltje) werd gemeten met een snelheid groter dan die van het licht (stukje in de wereld draait door). Achteraf bleek het een meetfout, maar de wereld van de natuurkunde stond even op zijn kop, omdat een vaste lichtsnelheid als een van de ijkpunten en grondvesten in de natuurkunde wordt gezien en zelfs contact maken met het verleden mogelijk zou zijn als deeltjes sneller zouden gaan! Het zou misschien leuk zijn om in je profielwerkstuk hier wat over te zeggen.

In Delft wordt momenteel niet gewerkt aan het meten van de snelheid van het licht, maar deze is wel belangrijk bij veel experimenten. De makkelijkste proef om deze te meten is met de magentronproef. Kijk voor dit proefje op deze site. Bekijk het filmpje en druk op lees verder om te kijken hoe dit in zijn werk gaat. Het enige wat je nodig hebt is een magnetron en een stuk chocolade!!

Andere manieren hoe wetenschappers vroeger hebben geprobeerd de lichtsnelheid te meten zijn ook erg intressant om te bekijken. Daarnaast zou ik goed zoeken op de woorden foton, licht en lichtsnelheid!

Succes en groetjes,

Michiel

We hoeven alleen te onderzoeken welk van de mogelijkheden we nodig hebben, maar we moeten wel alle mogelijkheden aan kunnen geven op basis van de informatie in de theoretische bronnen van ons profielwerkstuk. Daarom vragen we om info over de verschillende soorten windgeneratoren en turbines. Zo kunnen we een volledig beeld geven van wat er allemaal te vinden is van de onderdelen die we gebruiken en waarom we juist voor de onderdelen gekozen hebben die we uiteindelijk gebruiken.

Groetjes Marissa en Rob

Ik heb het even uitgezocht maar heb niet een twee drie iets kunnen vinden. Het makkelijkste is natuurlijk gewoon om naar je lokale elektronicaboer te gaan en het daar te halen (zij weten er ook veel vanaf en kunnen je met alles helpen). Anders kun je het ook op conrad.nl bestellen:

conrad osciallators.

Laat me maar weten als je nog vragen hebt!

Groetjes,
Ad

Misschien is het leuk om een vleermuisdetector te maken?

http://pw1.netcom.com/~t-rex/BatDetector.html

Vrij origineel lijkt me. Mocht je er niet uitkomen of vragen hebben dan hoor ik het graag!

Groeten,
Ad

He,

Weten jullie zeker of dat je deze materialen bij de TU Delft nodig hebt? Je zou heel makelijk zelf een plastic buis kunnen maken/regelen (bijvoorbeeld verschillende cola flessen zagen en aan elkaar maken). Als je afstand dan hoog genoeg is maakt je 'onzekerheid' van de stopwatch niet meer uit en heb je geen optische sensor nodig. Hoe willen jullie het proefje precies uitvoeren, hebben jullie al enig idee?

Groetjes,
Ad